The Segments Shown Below Could Form A Triangle - For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. A triangle cannot have a perimeter of length zero. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. The segments shown below could form a triangle. These segments could potentially form a triangle. Let's check if this condition is.
These segments could potentially form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. Let's check if this condition is. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. A triangle cannot have a perimeter of length zero. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. The segments shown below could form a triangle.
The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. These segments could potentially form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. A triangle cannot have a perimeter of length zero. The segments shown below could form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is.
The segments shown below could form a triangle. A с B 3 6 B C A O A
Let's check if this condition is. These segments could potentially form a triangle. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have.
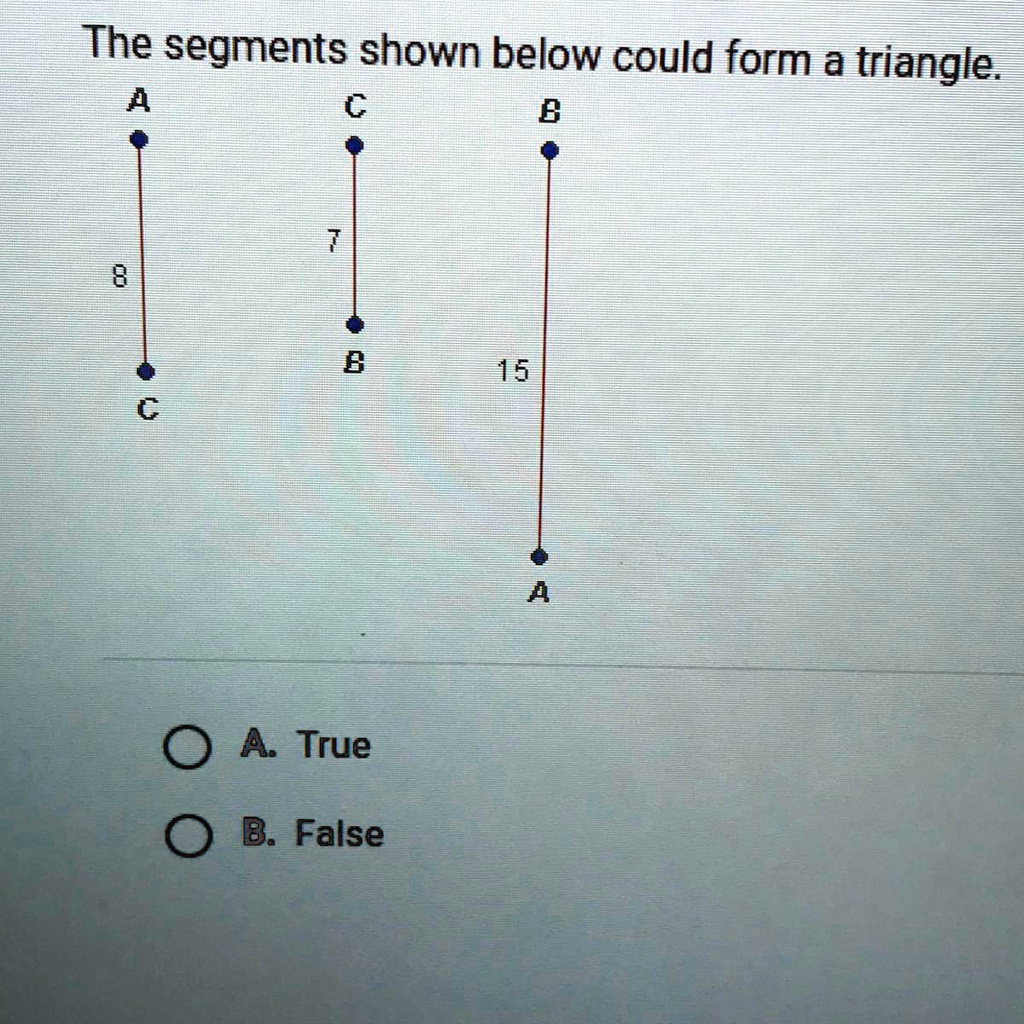
The segments shown below could form a triangle. True or False
To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. Let's check if this condition is. The segments shown below could form a triangle. These segments could potentially form a triangle. A triangle cannot have a perimeter of length zero.
The segments shown below could form a triangle.
The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have a perimeter of length zero. Let's check if this condition is. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side..
The segments shown below could form a triangle. д C B 9 11 B C O A
The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. A triangle cannot have a perimeter of length zero. The segments shown below could form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the.
The segments shown below could form a triangle. А С B 5 6 В 12 O A
For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. A triangle cannot have a perimeter of length zero. The segments shown below could form a triangle. Let's check if this condition is. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any.
the segments shown below could form a triangle ac9 cb7 ba16
Let's check if this condition is. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. A triangle cannot have a perimeter of length zero. The.
SOLVED 'The segments shown below could form a triangle. The segments
The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater than the. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. Let's check if this condition is. To form a triangle, the sum of the lengths of any.
The segments shown below could form a triangle. OA. True OB. False
To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. The segments shown below could form a triangle. A triangle cannot have a perimeter of length zero. The lengths given (ac=6, cb=5, ba=8) satisfy the triangle inequality theorem as the sum of any two sides is greater.
The segments shown below could form a triangle. A. True B. False
A triangle cannot have a perimeter of length zero. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. The segments shown below could form a triangle. To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third.
The segments shown below could form a triangle.True or False
The segments shown below could form a triangle. A triangle cannot have a perimeter of length zero. These segments could potentially form a triangle. Let's check if this condition is. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be.
The Lengths Given (Ac=6, Cb=5, Ba=8) Satisfy The Triangle Inequality Theorem As The Sum Of Any Two Sides Is Greater Than The.
To form a triangle, the sum of the lengths of any two sides must be greater than the length of the third side. For a set of three segments to form a triangle, the sum of the lengths of any two sides must be. These segments could potentially form a triangle. Let's check if this condition is.
The Segments Shown Below Could Form A Triangle.
A triangle cannot have a perimeter of length zero.