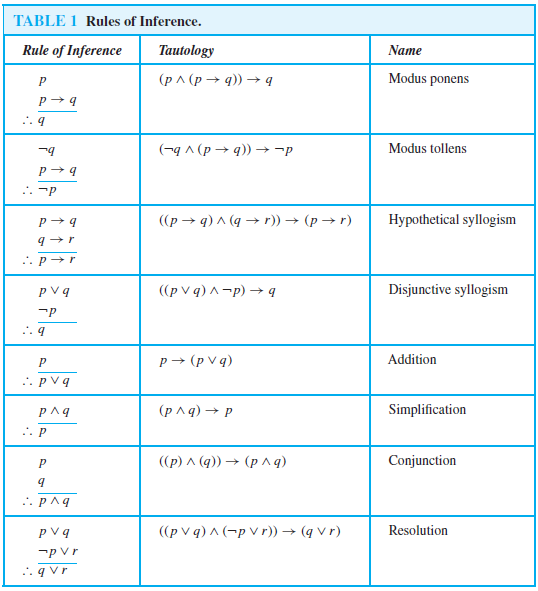
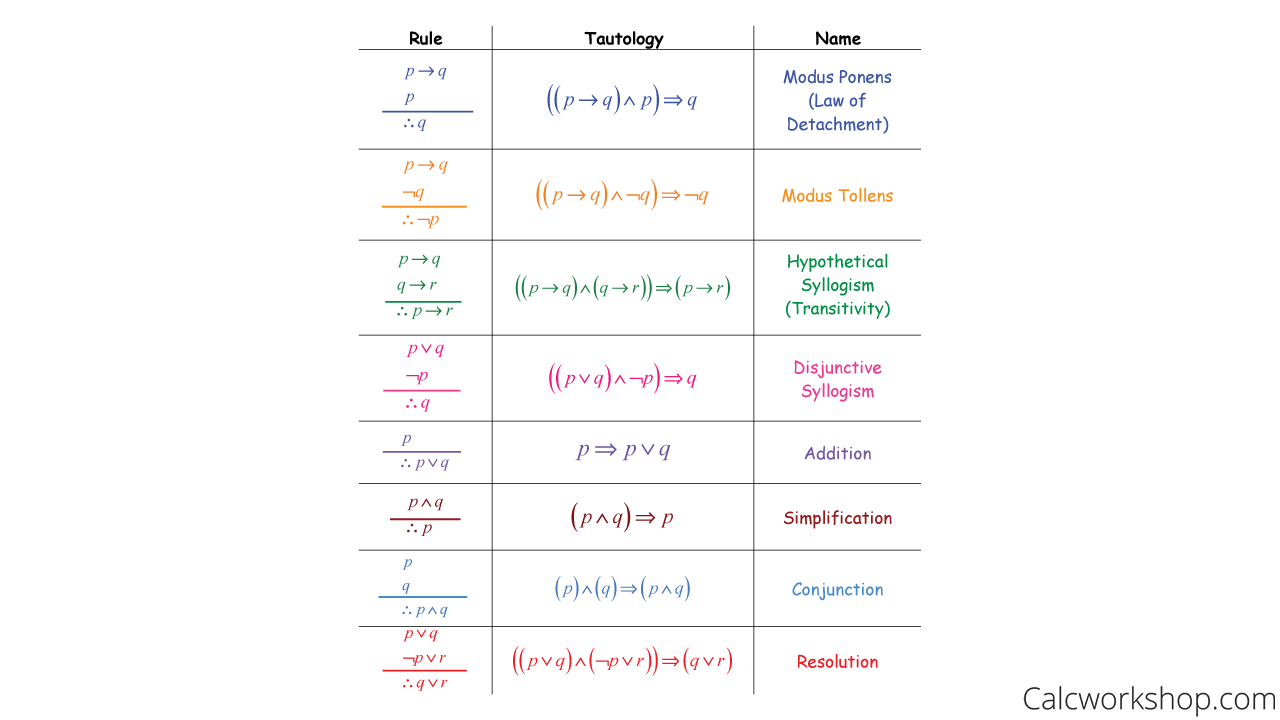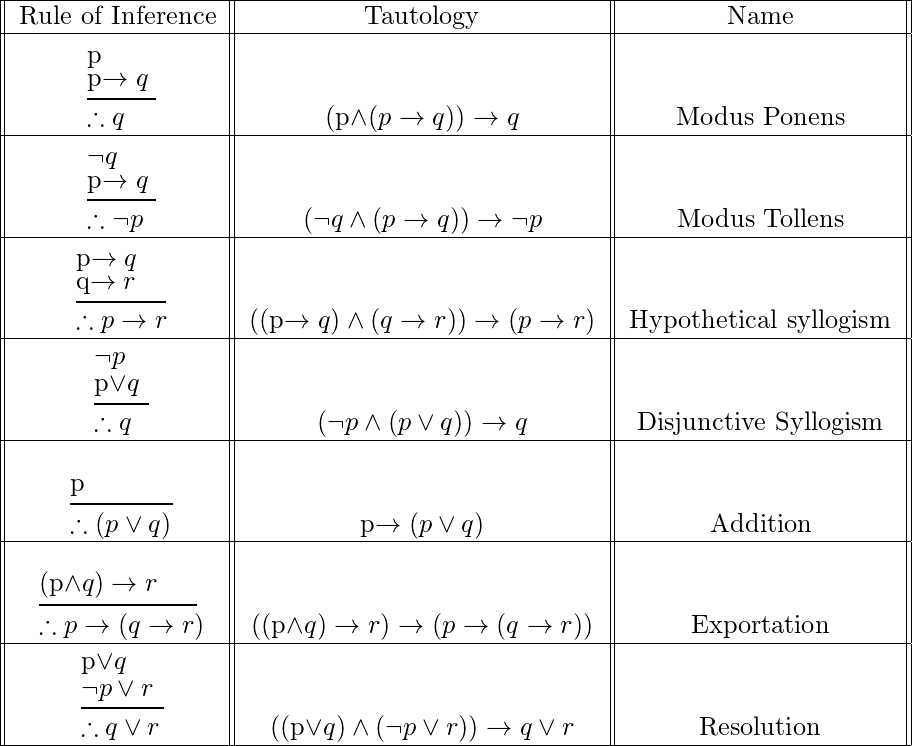Rules Of Inference Discrete Math - Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rather, the conclusion of a valid argument must be true if all the premises are. A valid argument does not always mean you have a true conclusion; There are various types of rules of inference, which are described as follows: Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a.
There are various types of rules of inference, which are described as follows: A valid argument does not always mean you have a true conclusion; Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a.
Suppose there are two premises, p and p → q. There are various types of rules of inference, which are described as follows: Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. A valid argument does not always mean you have a true conclusion; Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises.
Rules of Inference (Detailed w/ StepbyStep 7 Examples!)
Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. A valid argument does not always mean you have a true.
PPT Discrete Mathematics Rules of Inference and Proofs PowerPoint
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rather, the conclusion of a valid argument must be true if all the premises are. There are various types of rules of inference, which are described as follows: Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has.
Inference Rules Discrete Mathematics Lecture Slides Docsity
There are various types of rules of inference, which are described as follows: Suppose there are two premises, p and p → q. A valid argument does not always mean you have a true conclusion; Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rules of inference for quantifiers example 1 given.
Discrete Math 1 Tutorial 29 Rules of Inference YouTube
Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p → q. There are various types of rules of inference, which are described.
Rules_of_Inferences_Discrete_Mathematics_I_—_MATHCOSC_1056E_....pdf
Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Suppose there are two.
Proofs Unofficial UCSC Student Guide
Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p → q. Rules of inference are essential tools in logic and mathematics, enabling.
04 Rules of Inference and Proofs · Discrete Mathematics Explained in Detail
Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. There are various types of rules of inference, which are described.
RULES OF INFERENCE DISCRETE MATHEMATICS (Lesson Proper and Examples
A valid argument does not always mean you have a true conclusion; Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Rather, the conclusion of a valid argument.
PPT Discrete Mathematics PowerPoint Presentation ID264639
Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Suppose there are two premises, p and p → q. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rather, the conclusion of a valid argument must be.
Last Minute Notes Discrete Mathematics
There are various types of rules of inference, which are described as follows: Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rather, the conclusion of a valid argument must be true if all the premises are. Suppose there are two premises, p and p.
A Valid Argument Does Not Always Mean You Have A True Conclusion;
Rather, the conclusion of a valid argument must be true if all the premises are. Rules of inference for quantifiers example 1 given everyone in this discrete mathematics class has taken a course in computer science marla is a. Rules of inference are essential tools in logic and mathematics, enabling the derivation of conclusions from premises. Suppose there are two premises, p and p → q.