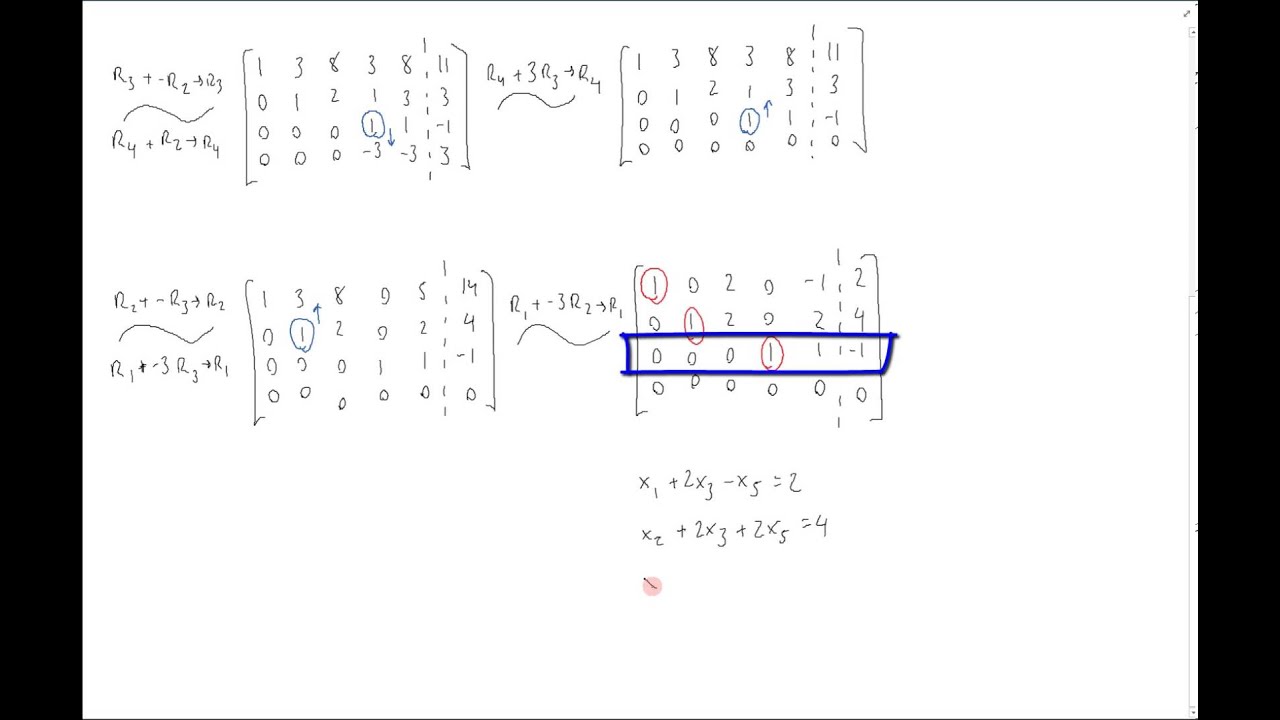
Parametric Vector Form Matrix

Parametric Vector Form Matrix - This is called a parametric equation or a parametric vector form of the solution. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. Suppose that the free variables in the homogeneous equation ax. Parametric vector form (homogeneous case) let a be an m × n matrix. The parameteric form is much more explicit: A common parametric vector form uses the free variables. It gives a concrete recipe for producing all solutions. You can choose any value for the free variables. Once you specify them, you specify a single solution to the equation.

Parametric vector form (homogeneous case) let a be an m × n matrix. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. The parameteric form is much more explicit: This is called a parametric equation or a parametric vector form of the solution. A common parametric vector form uses the free variables. You can choose any value for the free variables. Once you specify them, you specify a single solution to the equation. Suppose that the free variables in the homogeneous equation ax. As they have done before, matrix operations.

Parametric vector form (homogeneous case) let a be an m × n matrix. Suppose that the free variables in the homogeneous equation ax. As they have done before, matrix operations. The parameteric form is much more explicit: So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. It gives a concrete recipe for producing all solutions. A common parametric vector form uses the free variables. This is called a parametric equation or a parametric vector form of the solution. You can choose any value for the free variables.

Parametric vector form of solutions to a system of equations example

So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. A common parametric vector form uses the free variables. You can choose any value for the free variables. Suppose that the free variables in the homogeneous equation ax. Parametric vector form (homogeneous case) let a be an m × n matrix.

[Math] Parametric vector form for homogeneous equation Ax = 0 Math

Once you specify them, you specify a single solution to the equation. The parameteric form is much more explicit: So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. Suppose that the free variables in the homogeneous equation ax. A common parametric vector form uses the free variables.

Sec 1.5 Rec parametric vector form YouTube

Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. This is called a parametric equation or a parametric vector form of the solution. Once you specify them, you specify a single solution to the equation. A common parametric.

Example Parametric Vector Form of Solution YouTube

Once you specify them, you specify a single solution to the equation. A common parametric vector form uses the free variables. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. Suppose that the free variables in the homogeneous equation ax. You can choose any value for the free variables.

Parametric form solution of augmented matrix in reduced row echelon

Suppose that the free variables in the homogeneous equation ax. Once you specify them, you specify a single solution to the equation. As they have done before, matrix operations. Parametric vector form (homogeneous case) let a be an m × n matrix. A common parametric vector form uses the free variables.

Parametric Vector Form and Free Variables [Passing Linear Algebra

You can choose any value for the free variables. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. Once you specify them, you specify a single solution to the equation. A common parametric vector form uses the free.

1.5 Parametric Vector FormSolving Ax=b in Parametric Vector Form

The parameteric form is much more explicit: As they have done before, matrix operations. Suppose that the free variables in the homogeneous equation ax. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. This is called a parametric equation or a parametric vector form of the solution.

202.3d Parametric Vector Form YouTube

Suppose that the free variables in the homogeneous equation ax. Describe all solutions of $ax=0$ in parametric vector form, where $a$ is row equivalent to the given matrix. You can choose any value for the free variables. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. This is called a parametric equation or a parametric vector.

Solved Describe all solutions of Ax=0 in parametric vector

So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. As they have done before, matrix operations. A common parametric vector form uses the free variables. Parametric vector form (homogeneous case) let a be an m × n matrix. Suppose that the free variables in the homogeneous equation ax.

[Math] Parametric vector form for homogeneous equation Ax = 0 Math

A common parametric vector form uses the free variables. Suppose that the free variables in the homogeneous equation ax. You can choose any value for the free variables. As they have done before, matrix operations. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:.

A Common Parametric Vector Form Uses The Free Variables.

You can choose any value for the free variables. This is called a parametric equation or a parametric vector form of the solution. It gives a concrete recipe for producing all solutions. As they have done before, matrix operations.

Describe All Solutions Of $Ax=0$ In Parametric Vector Form, Where $A$ Is Row Equivalent To The Given Matrix.

Once you specify them, you specify a single solution to the equation. Parametric vector form (homogeneous case) let a be an m × n matrix. So subsitute $x_2 = s,x_4 = t$ and arrive at the parametrized form:. The parameteric form is much more explicit: