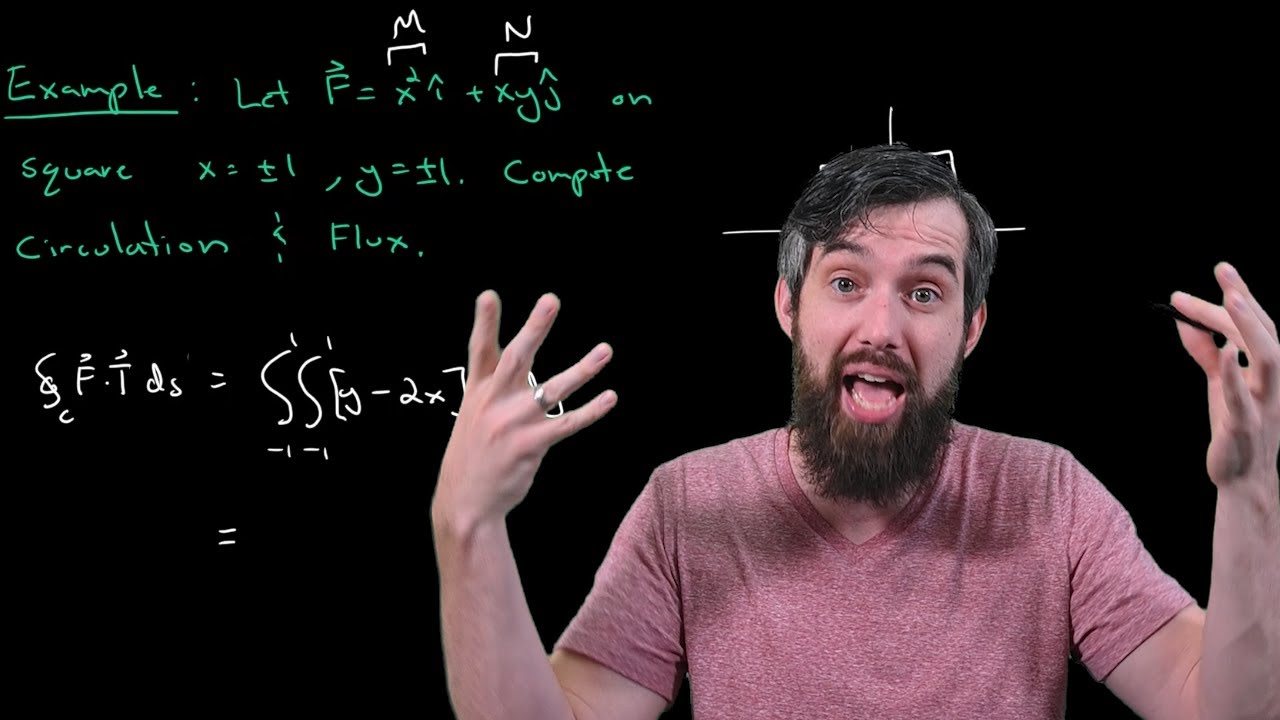Flux Form Of Green S Theorem - We substitute l(f) in place of f in equation (2) and use the. The flux of a fluid. The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. In a similar way, the flux form of green’s theorem follows from the circulation form: The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. Green's theorem can be used to find the area of a 2d shape.
The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. The flux of a fluid. In a similar way, the flux form of green’s theorem follows from the circulation form: We substitute l(f) in place of f in equation (2) and use the. Green's theorem can be used to find the area of a 2d shape. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\).
The flux of a fluid. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). We substitute l(f) in place of f in equation (2) and use the. Green's theorem can be used to find the area of a 2d shape. The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. In a similar way, the flux form of green’s theorem follows from the circulation form:
Green's Theorem Flux Form YouTube
The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. We substitute l(f) in place of f in equation (2) and use the. The flux of a fluid. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). In a similar way,.
Multivariable Calculus Green's Theorem YouTube
The flux of a fluid. We substitute l(f) in place of f in equation (2) and use the. The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). The flux form of green’s theorem relates.
Flux Form of Green's Theorem YouTube
The flux of a fluid. The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. Green's theorem can be used to find the area of a 2d shape. The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. The flux form of green’s theorem relates.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Hole
The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). Green's theorem can be used to find the area of a 2d shape. The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. The flux of a fluid. The integral we would.
Determine the Flux of a 2D Vector Field Using Green's Theorem
The flux of a fluid. In a similar way, the flux form of green’s theorem follows from the circulation form: We substitute l(f) in place of f in equation (2) and use the. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). Green's theorem can be used to find the.
The Green's Theorem Formula + Definition
The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. In a similar way, the flux form of green’s theorem follows from the circulation form: Green's theorem can be used to find the area of.
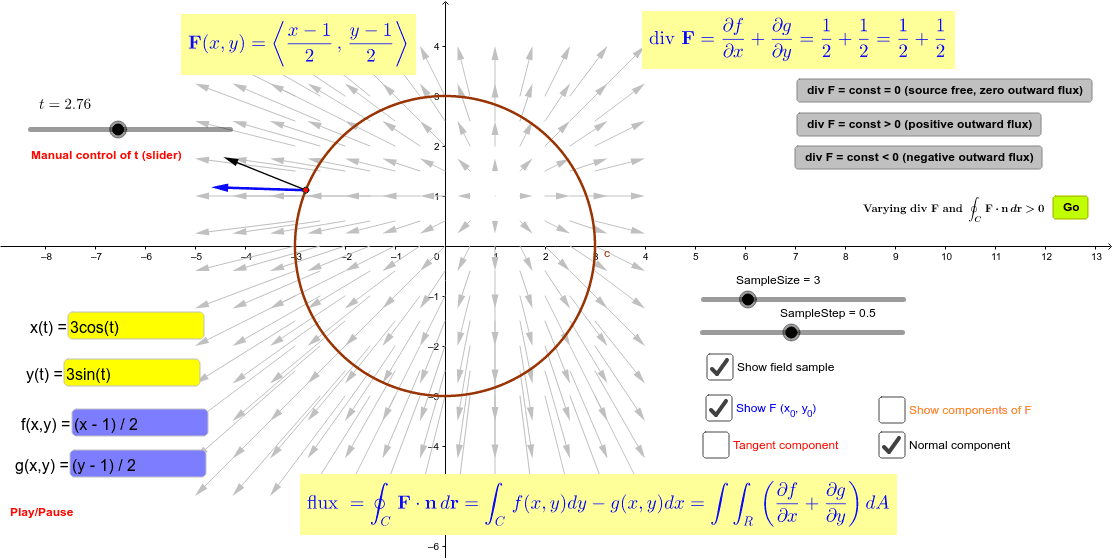
Illustration of the flux form of the Green's Theorem GeoGebra
Green's theorem can be used to find the area of a 2d shape. The flux of a fluid. The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). We substitute l(f) in place of f.
Flux Form of Green's Theorem Vector Calculus YouTube
The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). In a similar way, the flux form of green’s theorem follows from the circulation form: The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. We substitute l(f) in place of f in equation (2).
Example Using Green's Theorem to Compute Circulation & Flux // Vector
The flux of a fluid. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). Green's theorem can be used to find the area of a 2d shape. We substitute l(f) in place of f in equation (2) and use the. The integral we would normally use to calculate the area.
Determine the Flux of a 2D Vector Field Using Green's Theorem (Parabola
The flux of a fluid. The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex]. We substitute l(f) in place of f in equation (2) and use the. Green's theorem can be used to find the area of a 2d shape. The flux form of green’s theorem relates a double integral.
Green's Theorem Can Be Used To Find The Area Of A 2D Shape.
The integral we would normally use to calculate the area is just \iint_r 1\,da ∬ r1da. The flux form of green’s theorem relates a double integral over region \(d\) to the flux across boundary \(c\). In a similar way, the flux form of green’s theorem follows from the circulation form: We substitute l(f) in place of f in equation (2) and use the.
The Flux Of A Fluid.
The flux form of green’s theorem relates a double integral over region [latex]d[/latex] to the flux across curve [latex]c[/latex].