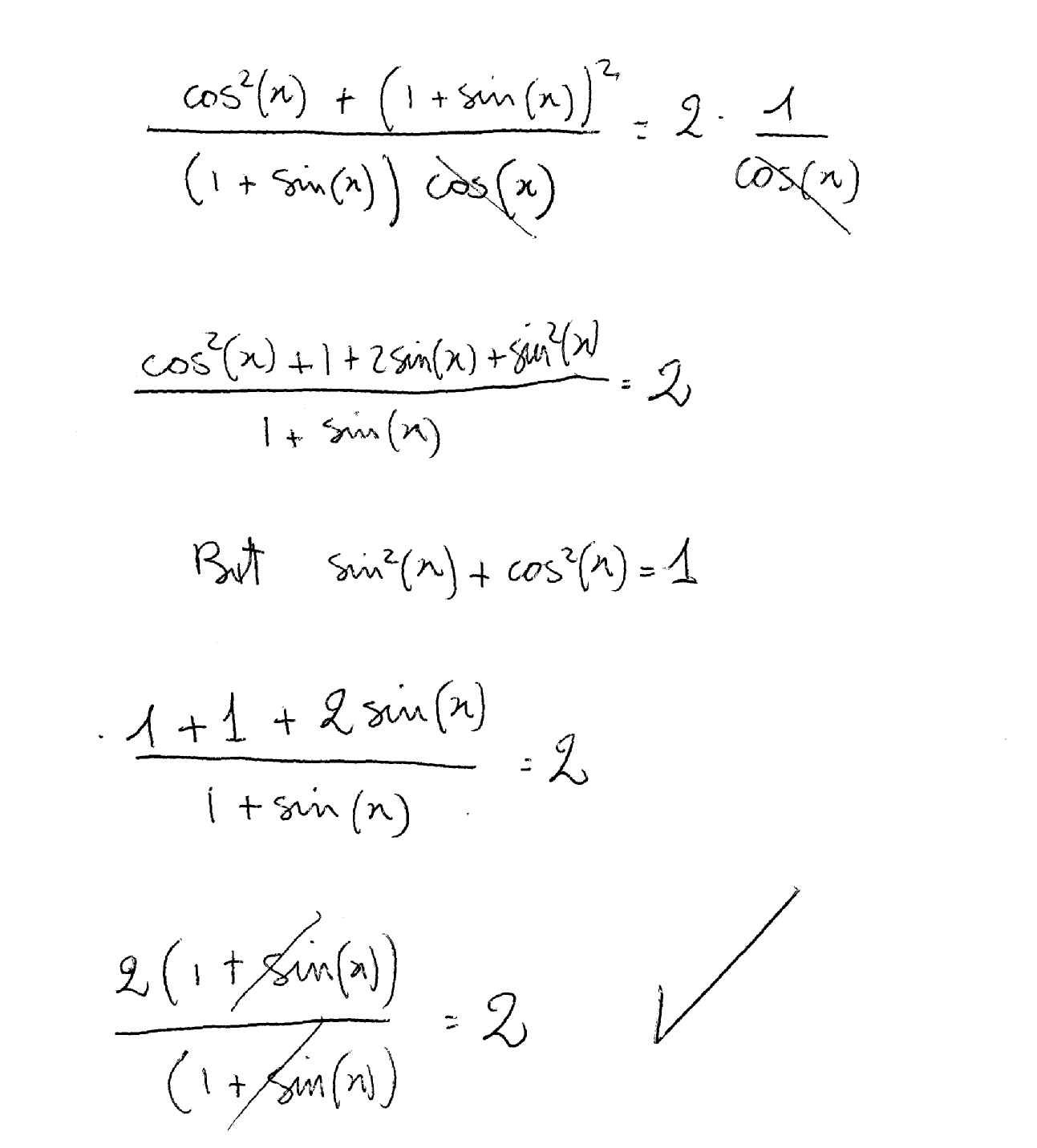Cosx Sinx - We can say it's a sum, i.e = cos x. We have, cos x sin x. Finding the value of cos x sin x: = 2 cos x sin x 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. Multiplying and dividing the given with 2.
Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. Multiplying and dividing the given with 2. Finding the value of cos x sin x: We can say it's a sum, i.e = cos x. = 2 cos x sin x 2. We have, cos x sin x.
We can say it's a sum, i.e = cos x. We have, cos x sin x. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. Finding the value of cos x sin x: = 2 cos x sin x 2. Multiplying and dividing the given with 2.
Trigonometric Identity (1 + cosx)/sinx + sinx/(1 + cosx) = 2/sinx YouTube
We have, cos x sin x. = 2 cos x sin x 2. Multiplying and dividing the given with 2. Finding the value of cos x sin x: Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1.
How do you verify this identity (cosx)/(1+sinx) + (1+sinx)/(cosx
We have, cos x sin x. Multiplying and dividing the given with 2. Finding the value of cos x sin x: Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. = 2 cos x sin x 2.
If y = (cosx + sinx)(cosx sinx) , prove that dydx = sec^2 (x + pi4 )
= 2 cos x sin x 2. We have, cos x sin x. Multiplying and dividing the given with 2. Finding the value of cos x sin x: We can say it's a sum, i.e = cos x.
Find the derivatives of sinx cosx Yawin
We can say it's a sum, i.e = cos x. Finding the value of cos x sin x: Multiplying and dividing the given with 2. = 2 cos x sin x 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1.
cosx^2+sinx^2=1
We can say it's a sum, i.e = cos x. Finding the value of cos x sin x: Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. We have, cos x sin x. = 2 cos x sin x 2.
Integral of (sinx + cosx)^2 YouTube
Multiplying and dividing the given with 2. = 2 cos x sin x 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. We can say it's a sum, i.e = cos x. We have, cos x sin x.
Misc 17 Find derivative sin x + cos x / sin x cos x
We can say it's a sum, i.e = cos x. = 2 cos x sin x 2. Multiplying and dividing the given with 2. We have, cos x sin x. Finding the value of cos x sin x:
y=(sinxcosx)^sinxcosx,Find dy/dx for the given function y wherever
Multiplying and dividing the given with 2. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1. We can say it's a sum, i.e = cos x. We have, cos x sin x. Finding the value of cos x sin x:
Cosxsinx/cosx+sinx simplify? YouTube
Finding the value of cos x sin x: We have, cos x sin x. Multiplying and dividing the given with 2. We can say it's a sum, i.e = cos x. Cos( x) = cos(x) sin( x) = sin(x) tan( x) = tan(x) double angle formulas sin(2x) = 2sinxcosx cos(2x) = (cosx)2 (sinx)2 cos(2x) = 2(cosx)2 1.
Find the minimum value of sinx cosx ? Brainly.in
We can say it's a sum, i.e = cos x. Multiplying and dividing the given with 2. Finding the value of cos x sin x: We have, cos x sin x. = 2 cos x sin x 2.
We Can Say It's A Sum, I.e = Cos X.
We have, cos x sin x. Multiplying and dividing the given with 2. Finding the value of cos x sin x: = 2 cos x sin x 2.